https://www.acmicpc.net/problem/1005
1005번: ACM Craft
첫째 줄에는 테스트케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 주어진다. 첫째 줄에 건물의 개수 N과 건물간의 건설순서 규칙의 총 개수 K이 주어진다. (건물의 번호는 1번부
www.acmicpc.net
1) 처음에는 위상정렬의 일부 개념(진입차수가 0인 노드부터 탐색)을 사용한 dfs 문제인 줄 알았으나
2) 위상정렬과 완전히 동일한 알고리즘을 구현하는 문제라고 깨달았다.
1)의 이유
-> 건설 과정에서 택하는 루트는 단 하나이다. 여러개의 루트로 가서 하나의 노드에서 만난다면 그 노드에서 택하는 이전 루트는 누적된 건설시간이 더 큰 하나의 루트이다. 즉 dfs 로 구현해야 한다고 판단하였다.
2)의 이유
-> 시작점이 1이라는 말이 없다. 이 말인 즉슨, 시작 노드를 택하는 것에는 어떤 우선순위가 존재하며 문제에서 주어진 예시가 방향그래프인 점을 감안하여 위상정렬에 의한 우선순위가 존재한다는 것을 짐작하였다.
또한 문제의 입력값은 반드시 사이클이 없는 방향그래프라는 점도 확인했다.
만약 사이클이 존재하는 경우, 어떤 방식으로도 노드의 시작점 우선순위를 알 수 없으며 동시에 목표 건물을 영원히 건설할 수 없는 상태가 된다.
문제에서 답이 존재 하지 않는 입력을 하지는 않을 것이기 때문에 일단 적어도 코드에서 사이클 여부를 확인할 필요는 없다.
위상정렬의 핵심 알고리즘은 다음과 같다.
1. 진입차수(들어오는 간선)가 0인 노드를 시작점으로 선택한다. (큐에 넣는다)
2. 큐에서 노드들을 꺼내어 차례대로 그래프에서 제거한다. 실제로 그래프를 수정하지는 않고 대신 노드들의 진출차수(나가는 간선)를 제거한다.
3. 다음 이동 노드의 진입차수가 0이 되면 큐에 넣는다.
4. 반복한다.
이렇게 진입차수가 0인 노드부터 탐색하여 순서가 결정되는 것이 위상정렬이다.
문제는 어떻게 위상정렬을 사용하여 하나의 루트로 이어지는 건설 순서를 구현할 것인가이다.
이를 위해 누적된 건설 시간을 기록하는 방식을 사용해 볼 수 있다.
다음 그래프를 보자.
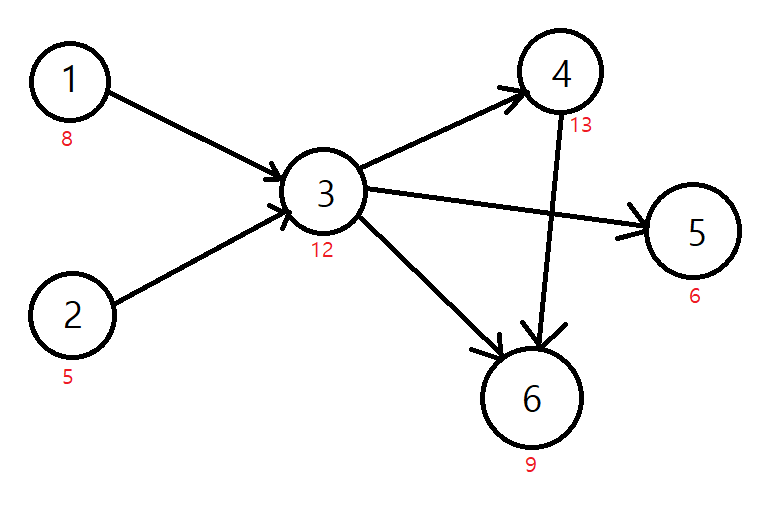
다시 문제의 정의를 생각해보자.
어떤 건물을 건설하기 위해서는 그 건물 이전에 존재하는 모든 건물의 건설이 끝나야 한다.
이는 어떤 건물 A의 진입차수가 0이 된 이후부터 건설이 가능하다는 얘기가 된다.
그래서 위 그래프에서 노드 1과 노드 2 중 건설 시간이 더 큰 노드 1의 건설만 완료되면 노드 3을 건설할 수 있는 것이다.
시작 노드는 1과 2가 된다.
여기서 노드 1을 탐색하고 그래프에서 지울 때 노드 3에게 1의 건설 시간을 넘겨줘야한다.
다음 노드 2를 탐색한 후 노드 3에게 건설 시간을 넘겨줄 때 노드 2는 노드 1보다 건설 시간이 짧으므로 넘겨줄 필요가 없다.
여기서 DP의 최대값 갱신을 써먹어 보는 것이다.
memo 배열을 선언하고 memo[i]를 "노드 i를 건설 완료했을 때 누적된 시간" 이라고 정의하자.
memo[i] = 노드 i를 건설 완료했을 때 누적된 시간
그러면 memo[3]은 처음에 갱신된 (노드 1과 노드 3의 건설 시간 합)인 8 + 12 = 20 보다 작은 (노드 2와 노드 3의 건설 시간 합) 5 + 12 로 바뀌지 않는다. 문제의 정의와 일치한다.
그렇게 건설 시간 합을 구하는 루트를 구해보면,
1 -> 3-> 4 -> 6
이 된다.
실제로는 6번 건물을 건설하기 위해 1, 2, 3, 4, 5번 건물 모두 건설한 것이지만
동시에 건물을 건설할 수 있는 경우가 있는데,
위상적으로 순서가 같은 경우에 놓인 건물들이 존재할 때(진입차수가 0인 건물들) 그 건물들은 동시에 건설할 수 있다.
위 그래프에서는 처음에 1과 2가 위상적으로 순서가 같고, 3입장에서 4와 5가 그러하다.
// BOJ GOLD 3
// https://www.acmicpc.net/problem/1005
#include <bits/stdc++.h>
using namespace std;
int buildtime[1001];
int indegree[1001];
int memo[1001];
int main(int argc, char** argv) {
ios_base::sync_with_stdio(0); cin.tie(0);
int t; cin >> t;
while (t--) {
int n, k; cin >> n >> k;
vector<vector<int>> graph(n + 1);
for (int i = 0; i < n; i++) {
cin >> buildtime[i + 1];
memo[i + 1] = buildtime[i + 1];
}
for (int i = 0; i < k; i++) {
int a, b; cin >> a >> b;
graph[a].push_back(b);
indegree[b]++;
}
int target; cin >> target;
queue<int> q;
for (int i = 1; i <= n; i++) {
if (indegree[i] == 0) q.push(i);
}
while (!q.empty()) {
int cur = q.front(); q.pop();
for (int& next : graph[cur]) {
memo[next] = max(memo[next], memo[cur] + buildtime[next]);
if (--indegree[next] == 0) {
q.push(next);
}
}
}
memset(buildtime, 0, sizeof(buildtime));
memset(indegree, 0, sizeof(indegree));
cout << memo[target] << '\n';
}
return 0;
}'Algorithms' 카테고리의 다른 글
| [백준 #12100 c++] 2048 easy (1) | 2024.01.20 |
|---|---|
| [백준 #1967 c++] 트리의 지름, 증명하기 (1) | 2024.01.15 |
| [백준 #2096 c++] 내려가기 (1) | 2023.11.26 |
| [백준 #14502 c++] 연구소 (0) | 2023.11.23 |
| [백준 #11758 c++] CCW (0) | 2023.11.19 |
